HSLD(Heat Source Layout Dataset)数据集
HSLD 数据集描述热源系统区域为 0.1m×0.1m 的矩形,且离散化为 200×200 的网格。数据集共提供 Case 1、Case 2 和 Case 3 三个子数据集。每个子数据集含有 2000 组训练样本(由 Sequence 采样生成),40000 组测试样本(Test 1,2 分别为 Sequence 采样和 Gibbs 采样生成的测试样本,Test 3, 4, 5, 6, 7, 8, 9 为特殊测试样本)。
- Generality
三种典型热传导问题
- Case 1: 狄利克雷边界条件下的体边散热问题
- Case 2:狄利克雷和纽曼混合边界下的体边散热问题
- Case 3:狄利克雷和纽曼混合边界下的体点散热问题
- Reasonability
HSLD 数据库设计合理(2000 组训练样本,40000 组多样化测试样本的数据集)
- Diversity
边界条件和组件多样性且提供多样性评价准则
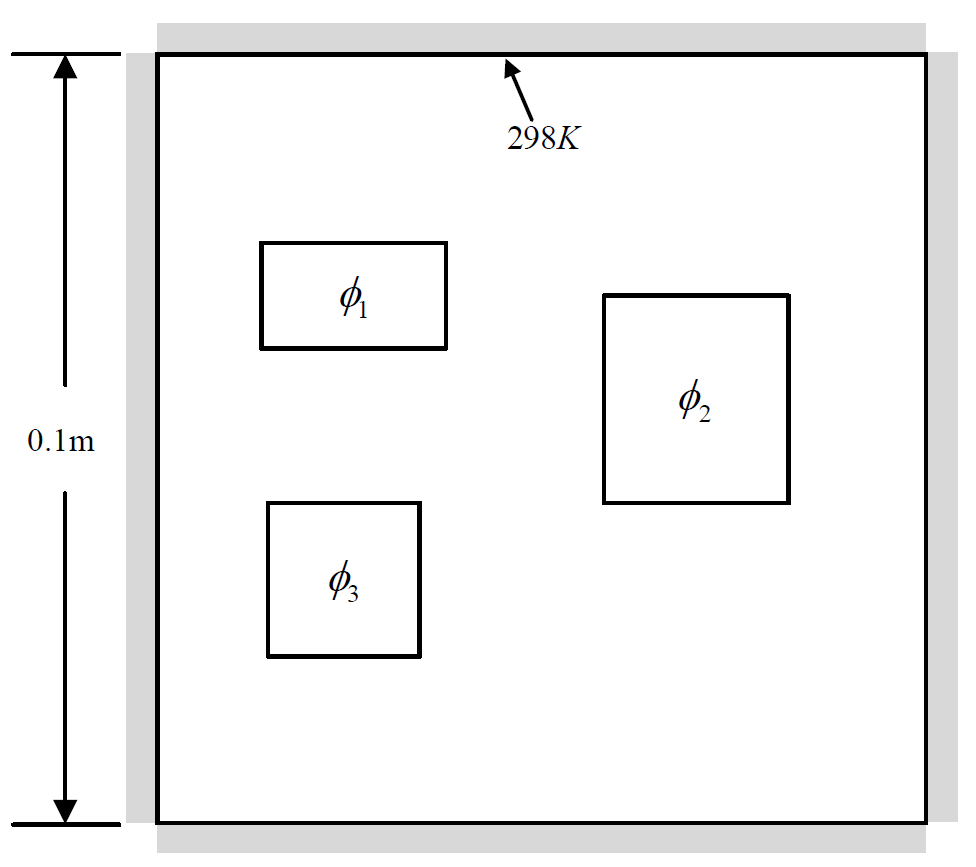
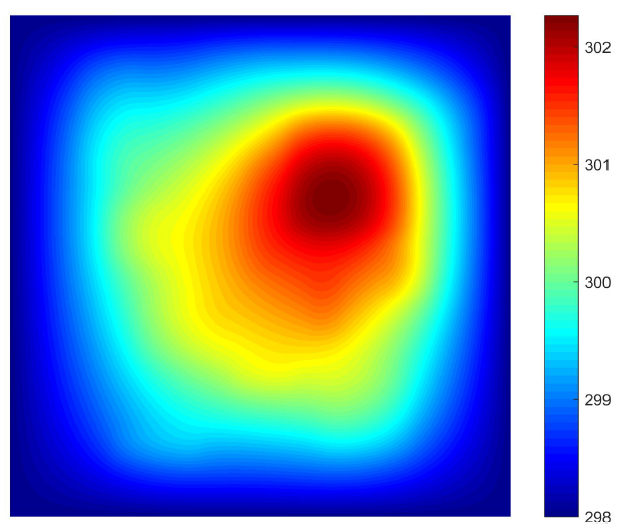
Case 1 子数据集
四周散热的热传导问题,四边均为狄利克雷边界条件(Dirichlet BC),恒温为 298K
 |
 |
 |
|---|---|---|
| 边界条件 | 组件布局信息 | 温度场 |
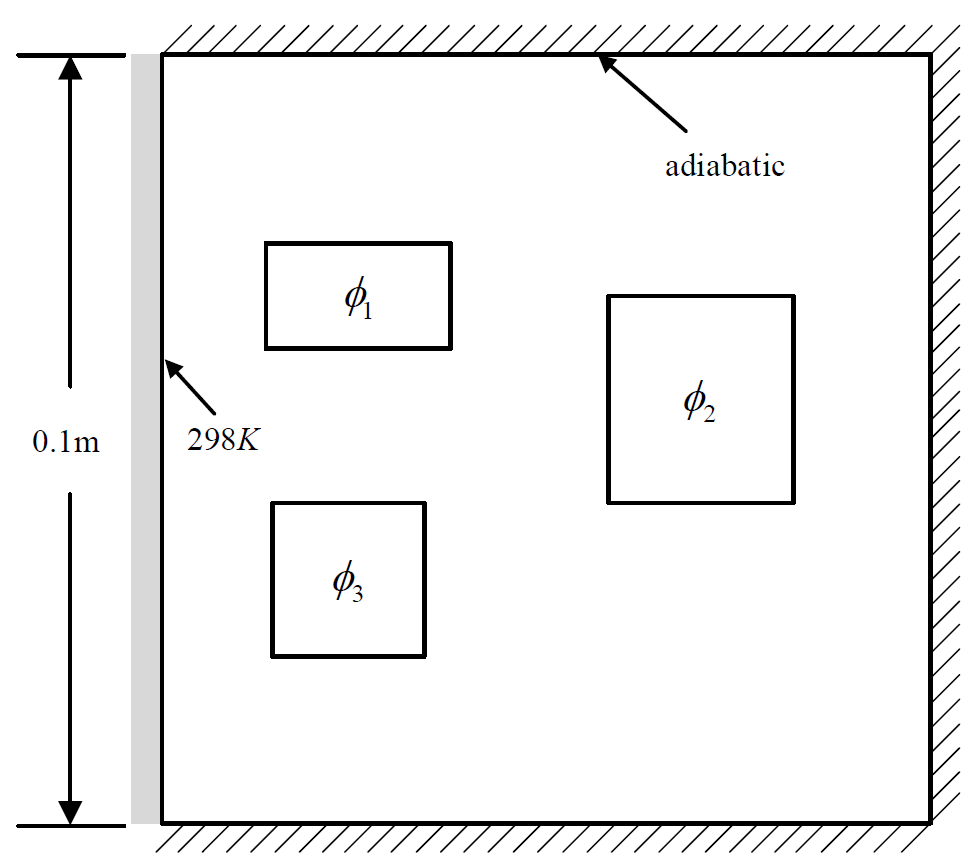
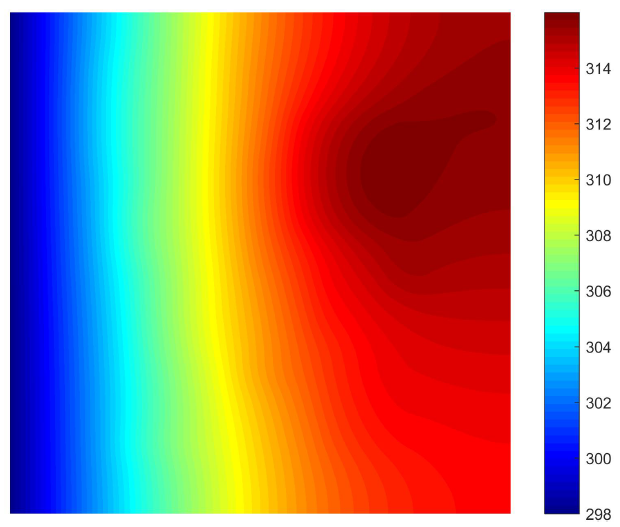
Case 2 子数据集
单边散热的热传导问题,左边界恒温为 298K(Dirichlet BC),其他边界是绝热的(Neumann BC)
 |
 |
 |
|---|---|---|
| 边界条件 | 组件布局信息 | 温度场 |
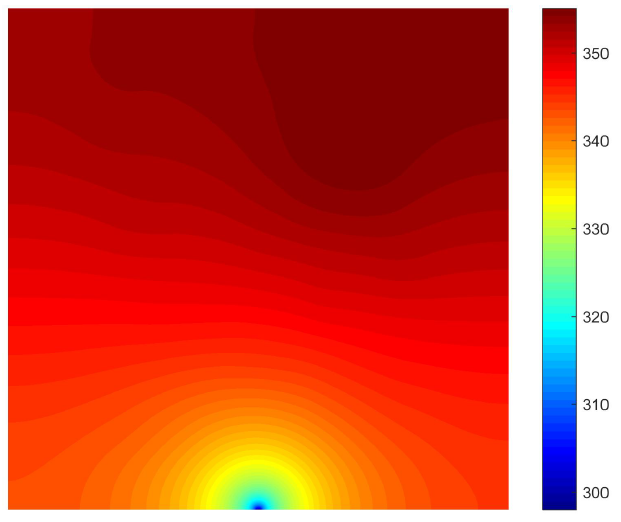
Case 3 子数据集
小孔散热的热传导问题,散热器的宽度设置为 0.001m,恒温值为 298K (Dirichlet BC),其他边界是绝热的(Neumann BC)
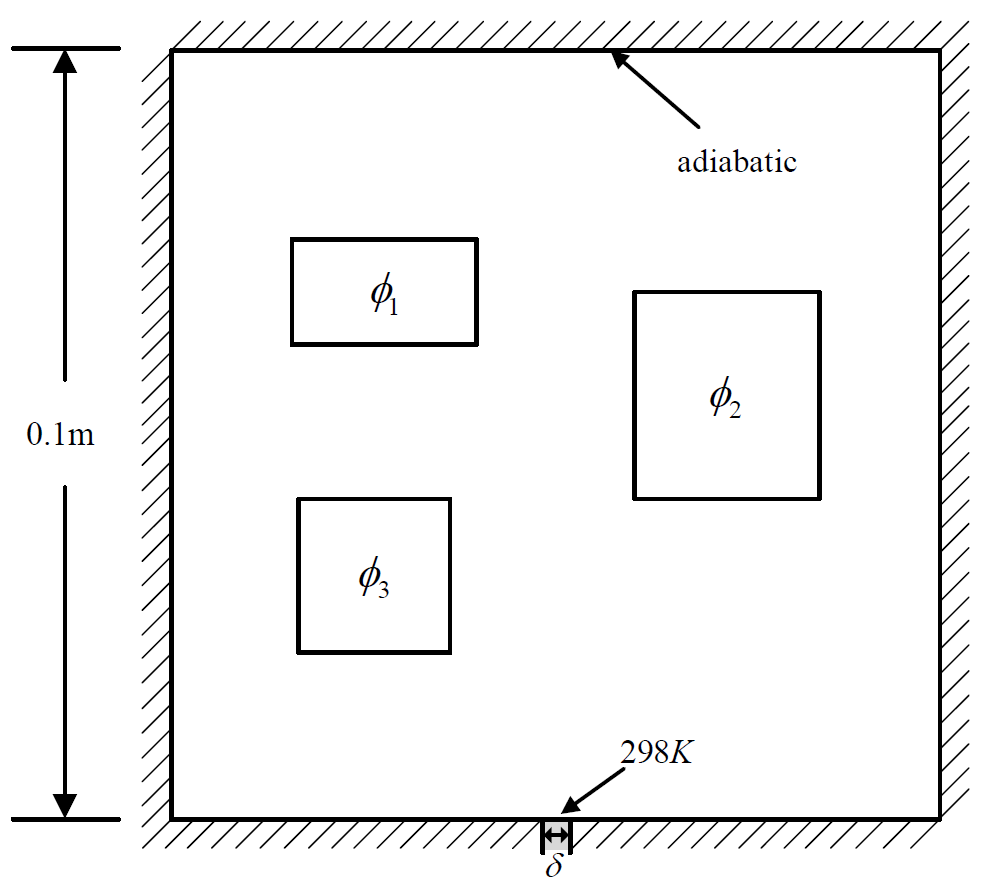 |
 |
 |
|---|---|---|
| 边界条件 | 组件布局信息 | 温度场 |
特殊布局样本
分别从功耗影响最大组件位置、相同功率组件相对位置、受限组件布局区域等角度出发生成 7 种不同类型的特殊布局测试样本.
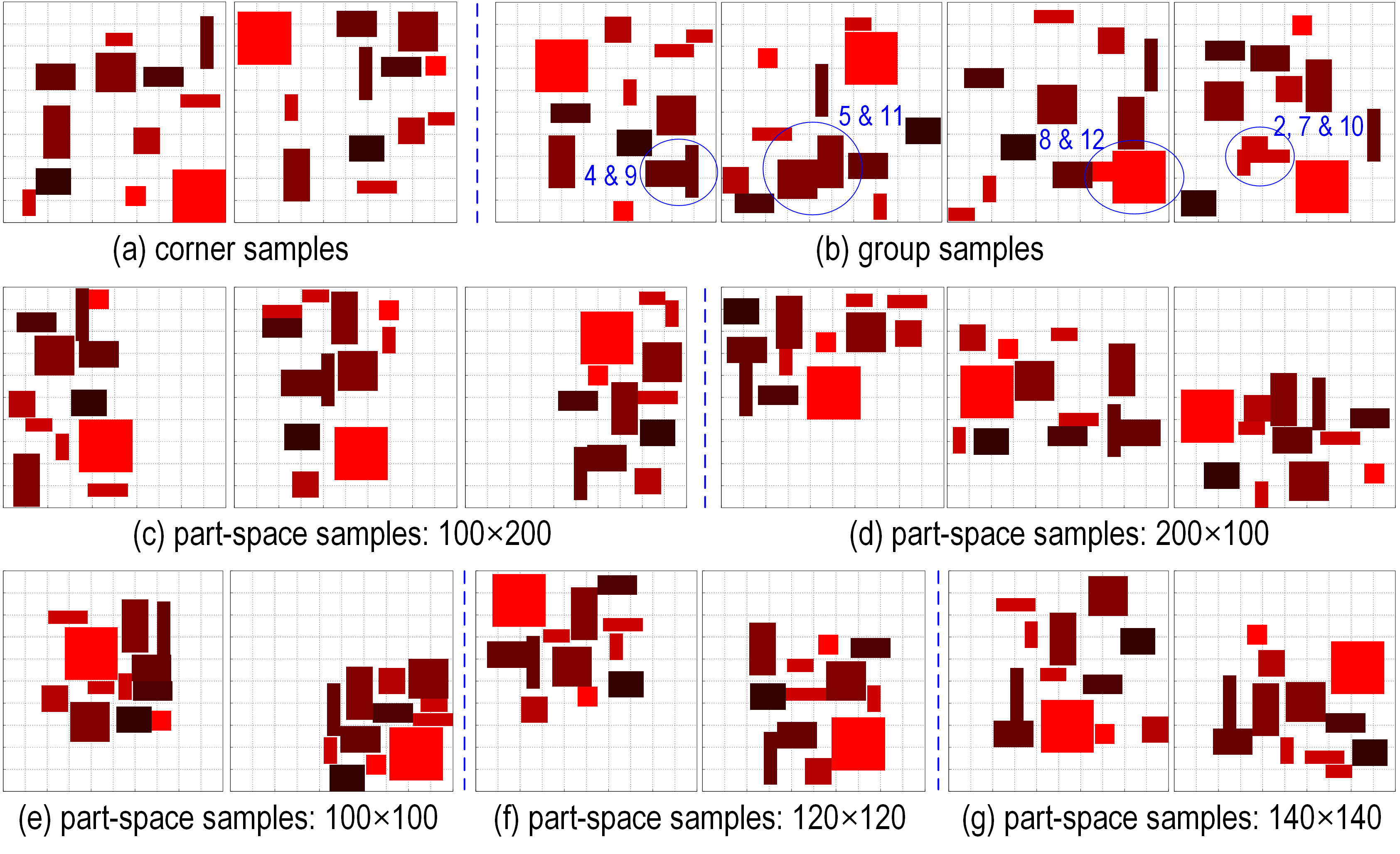
测试集说明
测试集中一共包含 9 个子测试集,一共 40000 组测试样本,旨在尽可能对代理模型的全局预测性能进行评价。
| 测试集 | 样本数量 | 类型 |
|---|---|---|
| 1 | 10000 | Sequence layout samples |
| 2 | 10000 | Gibbs layout samples |
| 3 | 1000 | Corner samples |
| 4 | 1000×4 | Group samples |
| 5 | 1000×6 | Part-space samples: 200×100 |
| 6 | 1000×6 | Part-space samples: 100×200 |
| 7 | 1000 | Part-space samples: 140×140 |
| 8 | 1000 | Part-space samples: 120×120 |
| 9 | 1000 | Part-space samples: 100×100 |
数据说明
样本采用.mat 格式存储
- 'u':{ndarray:200,200},温度场数据,取值范围298-
- 'F':{ndarray:200,200},布局数据,取值范围0-20000
- 'xs':{ndarray: 200 , 200 },温度点x轴坐标数据,取值范围0-0.1
- 'ys':{ndarray: 200 , 200 },温度点y轴坐标数据,取值范围0-0.1
评价准则
像素级评价指标(Pixel-level metrics)
最高温度绝对误差(MT-AE)
预测温度场最高温度处绝对误差
最高温位置绝对误差(MT-PAE)
预测温度场最高温度处位置绝对误差
图像级评价指标(Image-level metrics)
平均绝对误差(MAE)
预测温度场绝对误差的平均值
最大绝对误差(Max-AE)
预测温度场绝对误差最大值
Dirichlet 边界平均绝对误差(BMAE_D)
Dirichlet 边界处预测温度场误差平均值
Neumann 边界平均绝对误差(BMAE_N)
Neumann 边界处预测温度场误差平均值
组件平均绝对误差(CMAE)
组件布局区域预测温度场误差平均值
梯度平均绝对误差(G-MAE)
利用沿两个方向(横轴和纵轴)的中心差值计算温度分布梯度场平均误差值
Laplace 平均绝对误差(Lap-MAE)
预测温度场的拉普拉斯算子平均绝对误差
批块级评价指标(Batch-level metrics)
预测最高温排序的斯皮尔曼相关系数
关于不同布局样本的预测温度场最高温的大小顺序相关性